Logistic Regression Example

The Dataset

The data is a mixed variable dataset containing 14 variables of 297 patients for their heart disease diagnosis. The data comes in an R package called kmed which you can read about on your own. Patients were diagnosed with heart disease in four classes. We will used this dataset to illustrate how multiple risk factors are related to a heart disease diagnosis, such as age (years), sex (FALSE = female; TRUE = male), chest pain (1 = typical angina, 2 = atypical angina, 3 = non-anginal pain, and 4 = asymptomatic) and thalach (max heart rate achieved).

library(kmed)
dat <- heart

# select variables
library(dplyr)
dat <- dat %>%
  dplyr::select(
    age,
    sex,
    cp,
    thalach,
    class
  )
# print dataset's structure
str(dat)

'data.frame':   297 obs. of  5 variables:
 $ age    : num  63 67 67 37 41 56 62 57 63 53 ...
 $ sex    : logi  TRUE TRUE TRUE TRUE FALSE TRUE ...
 $ cp     : Factor w/ 4 levels "1","2","3","4": 1 4 4 3 2 2 4 4 4 4 ...
 $ thalach: num  150 108 129 187 172 178 160 163 147 155 ...
 $ class  : int  0 2 1 0 0 0 3 0 2 1 ...
 - attr(*, "na.action")= 'omit' Named int [1:6] 88 167 193 267 288 303
  ..- attr(*, "names")= chr [1:6] "88" "167" "193" "267" ...

# rename variables
dat <- dat %>%
  dplyr::rename(
    chest_pain = cp,
    max_heartrate = thalach,
    heart_disease = class
  )

# recode sex
dat$sex <- factor(dat$sex,
  levels = c(FALSE, TRUE),
  labels = c("female", "male")
)

# recode chest_pain
dat$chest_pain <- factor(dat$chest_pain,
  levels = 1:4,
  labels = c("typical angina", "atypical angina", "non-anginal pain", "asymptomatic")
)

# recode heart_disease into 2 classes
dat$heart_disease <- ifelse(dat$heart_disease == 0,
  0,
  1
)

# set labels for heart_disease
dat$heart_disease <- factor(dat$heart_disease,
  levels = c(0, 1),
  labels = c("no disease", "disease")
)

levels(dat$heart_disease)

[1] "no disease" "disease"

# save model
m1 <- glm(heart_disease ~ age,
  data = dat,
  family = "binomial"
)

summary(m1)


Call:
glm(formula = heart_disease ~ age, family = "binomial", data = dat)

Coefficients:
            Estimate Std. Error z value Pr(>|z|)    
(Intercept) -3.05122    0.76862  -3.970  7.2e-05 ***
age          0.05291    0.01382   3.829 0.000128 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 409.95  on 296  degrees of freedom
Residual deviance: 394.25  on 295  degrees of freedom
AIC: 398.25

Number of Fisher Scoring iterations: 4

# OR for age
exp(coef(m1)["age"])

     age 
1.054331

# prob(heart disease) for age = 0
exp(coef(m1)[1]) / (1 + exp(coef(m1)[1]))

(Intercept) 
 0.04516478

# 95% CI for the OR for age
exp(confint(m1,
  parm = "age"
))

   2.5 %   97.5 % 
1.026699 1.083987

# predict probability to develop heart disease
pred <- predict(m1,
  newdata = data.frame(age = c(30)),
  type = "response"
)

pred

        1 
0.1878525

# predict probability to develop heart disease
pred <- predict(m1,
  newdata = data.frame(age = c(30)),
  type = "response",
  se = TRUE
)

pred$fit

        1 
0.1878525

# 95% confidence interval for the prediction
lower <- pred$fit - (qnorm(0.975) * pred$se.fit)
upper <- pred$fit + (qnorm(0.975) * pred$se.fit)
c(lower, upper)

         1          1 
0.07873357 0.29697138

# 95% confidence interval for the prediction
lower <- pred$fit - (1.96 * pred$se.fit)
upper <- pred$fit + (1.96 * pred$se.fit)
c(lower, upper)

         1          1 
0.07873156 0.29697339

library(sjPlot)

Install package "strengejacke" from GitHub (`devtools::install_github("strengejacke/strengejacke")`) to load all sj-packages at once!

library(ggplot2)

# plot
plot_model(m1,
  type = "pred",
  terms = "age"
) +
  labs(y = "Prob(heart disease)") + theme_bw()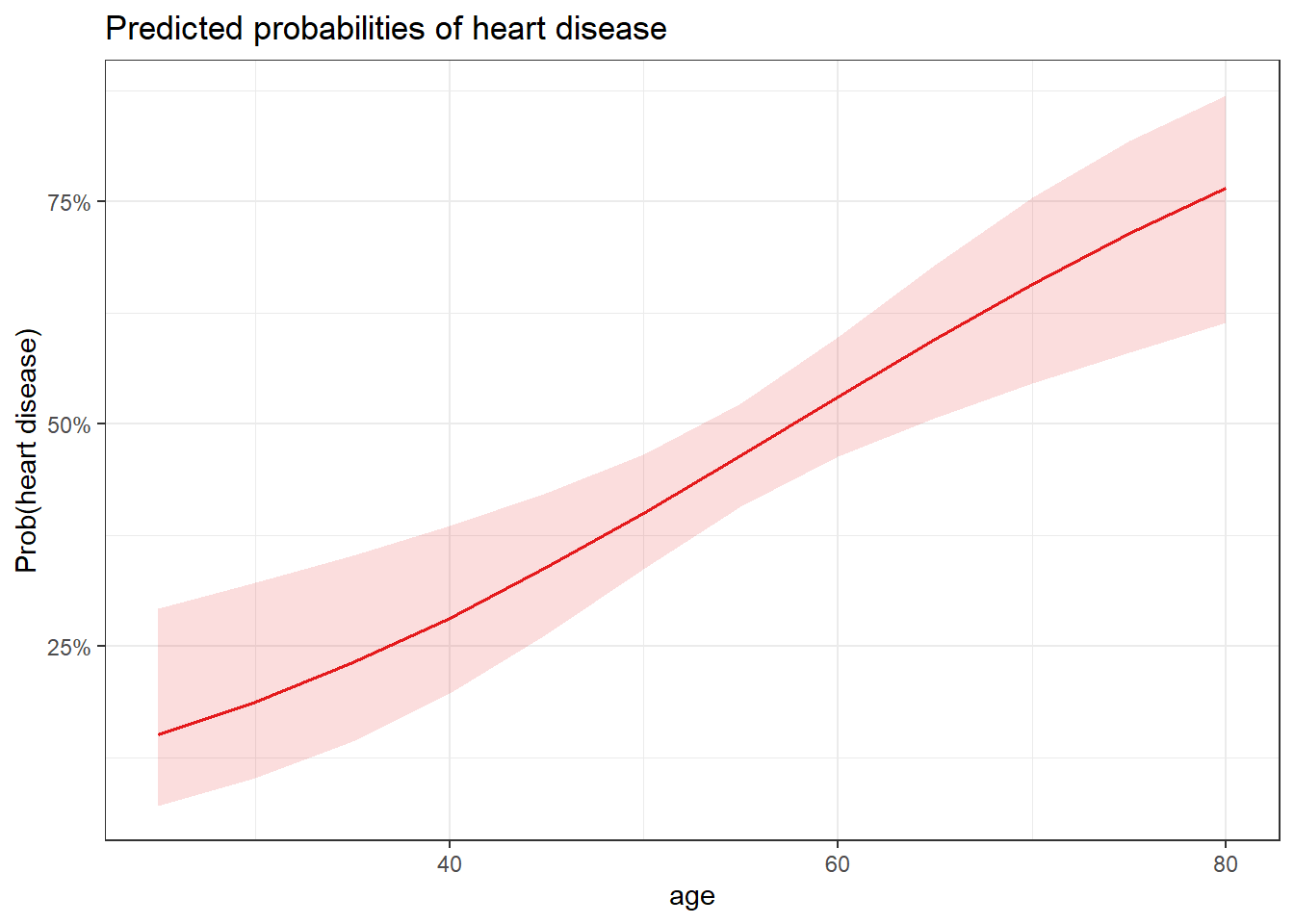

# levels for sex
levels(dat$sex)

[1] "female" "male"

# save model
m2 <- glm(heart_disease ~ sex,
  data = dat,
  family = "binomial"
)

summary(m2)


Call:
glm(formula = heart_disease ~ sex, family = "binomial", data = dat)

Coefficients:
            Estimate Std. Error z value Pr(>|z|)    
(Intercept)  -1.0438     0.2326  -4.488 7.18e-06 ***
sexmale       1.2737     0.2725   4.674 2.95e-06 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 409.95  on 296  degrees of freedom
Residual deviance: 386.12  on 295  degrees of freedom
AIC: 390.12

Number of Fisher Scoring iterations: 4

exp(coef(m2)["sexmale"])

 sexmale 
3.573933

# prob(disease) for sex = female
exp(coef(m2)[1]) / (1 + exp(coef(m2)[1]))

(Intercept) 
  0.2604167

chisq.test(table(dat$heart_disease, dat$sex))


    Pearson's Chi-squared test with Yates' continuity correction

data:  table(dat$heart_disease, dat$sex)
X-squared = 21.852, df = 1, p-value = 2.946e-06

# predict probability to develop heart disease
pred <- predict(m2,
  newdata = data.frame(sex = c("male")),
  type = "response"
)
pred

        1 
0.5572139

# plot
plot_model(m2,
  type = "pred",
  terms = "sex"
) +
  labs(y = "Prob(heart disease)")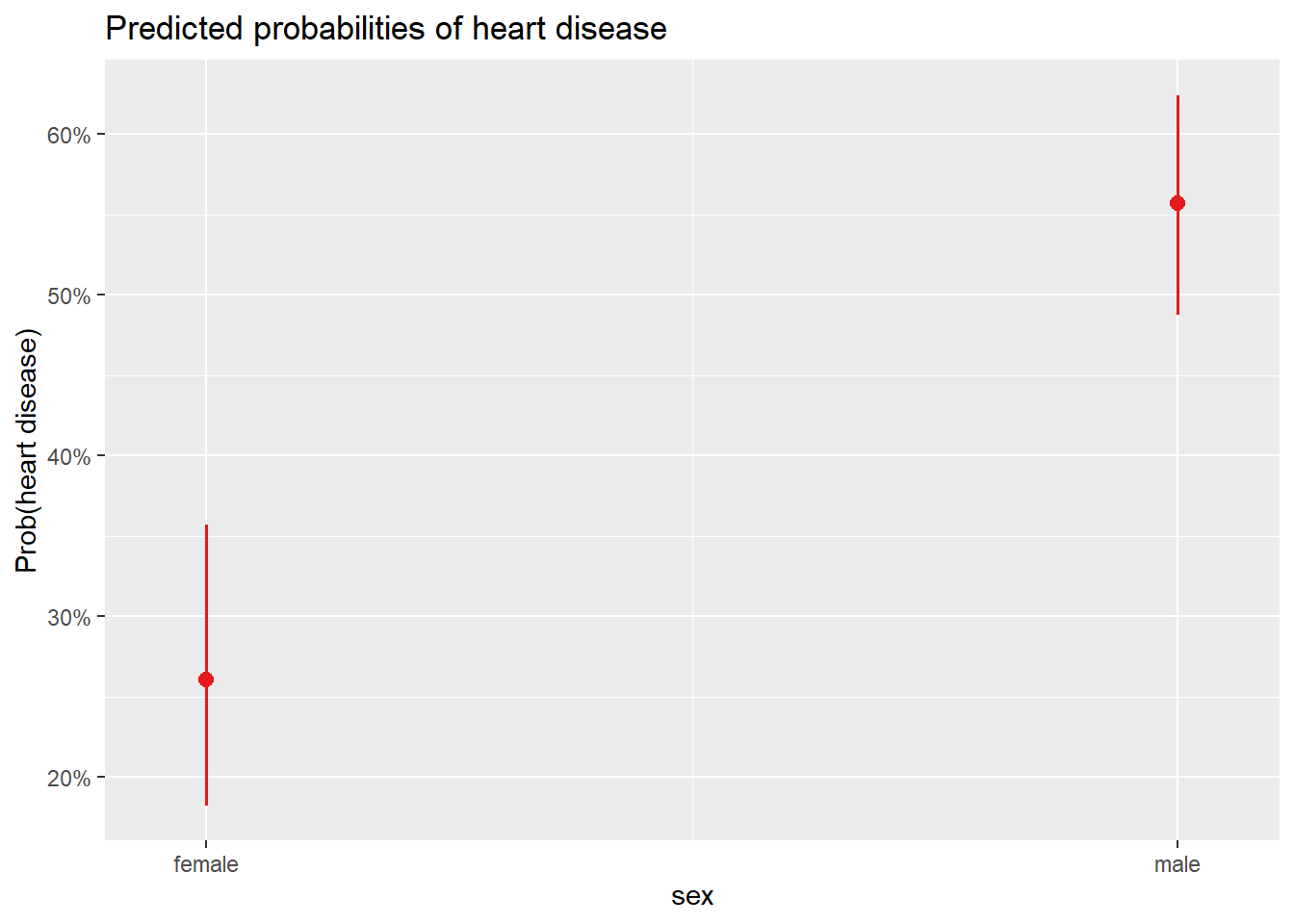

# create data frame of new patient
new_patient <- data.frame(
  age = 32,
  sex = "female"
)

m3 <- glm(heart_disease ~ sex + age,
  data = dat,
  family = "binomial"
)
# predict probability to develop heart disease
pred <- predict(m3,
  newdata = new_patient,
  type = "response"
)
# print prediction
pred

         1 
0.06224456

# 1. age, sex and chest pain on prob of disease
plot_model(m3,
  type = "pred",
  terms = c("age",  "sex"),
  ci.lvl = NA # remove confidence bands
) +
  labs(y = "Prob(heart disease)")

Data were 'prettified'. Consider using `terms="age [all]"` to get smooth
  plots.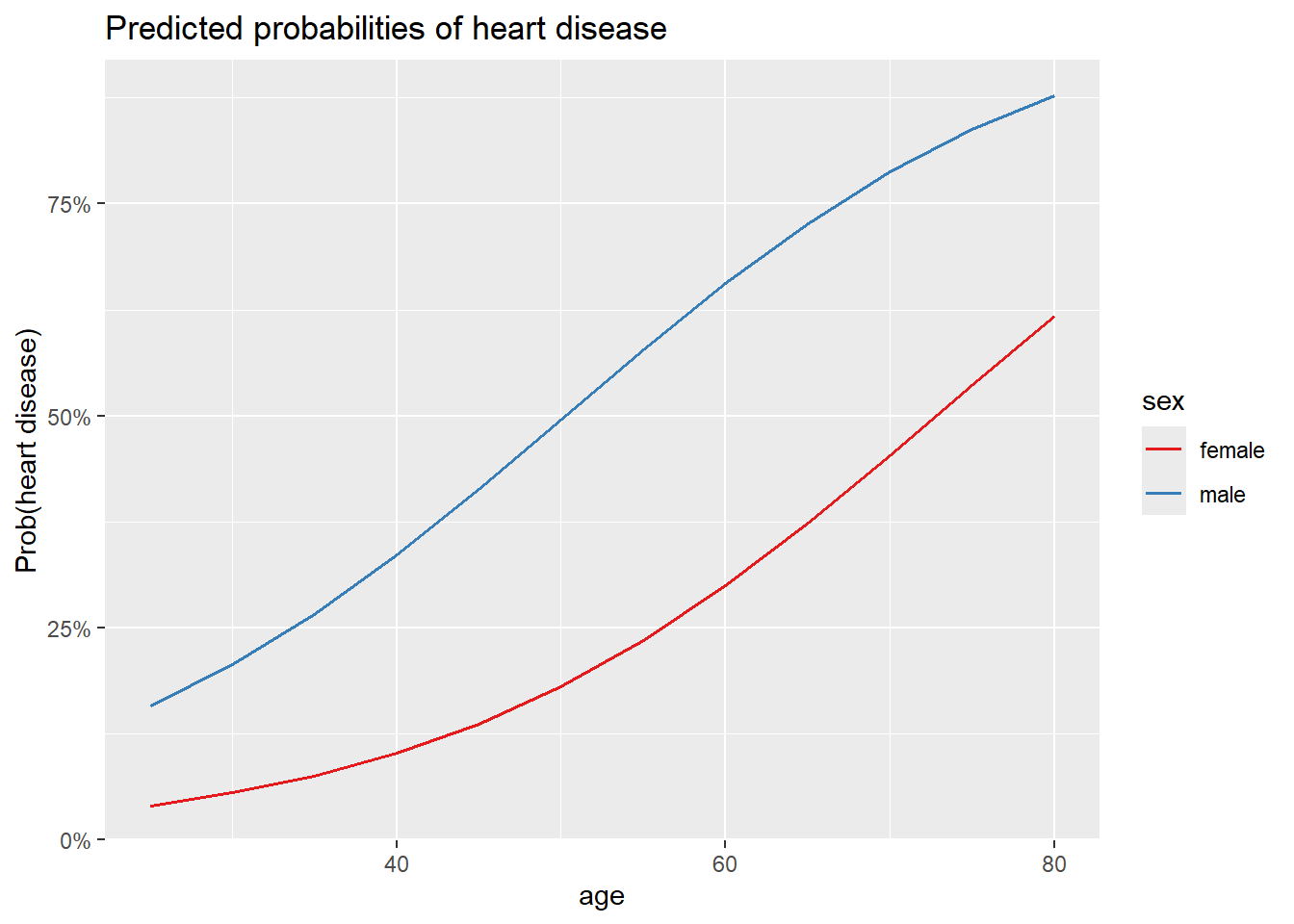

tab_model(m3, m2,
  show.ci = FALSE, # remove CI
  show.aic = TRUE, # display AIC
  p.style = "numeric_stars" # display p-values and stars
)

	heart disease		heart disease
Predictors	Odds Ratios	p	Odds Ratios	p
(Intercept)	0.01 ^***	<0.001	0.35 ^***	<0.001
sex [male]	4.47 ^***	<0.001	3.57 ^***	<0.001
age	1.07 ^***	<0.001
Observations	297		297
R² Tjur	0.142		0.078
AIC	370.435		390.118
* p<0.05 p<0.01 * p<0.001

library(pROC)

# save roc object
res <- roc(heart_disease ~ fitted(m3),
  data = dat
)
# plot ROC curve
ggroc(res, legacy.axes = TRUE)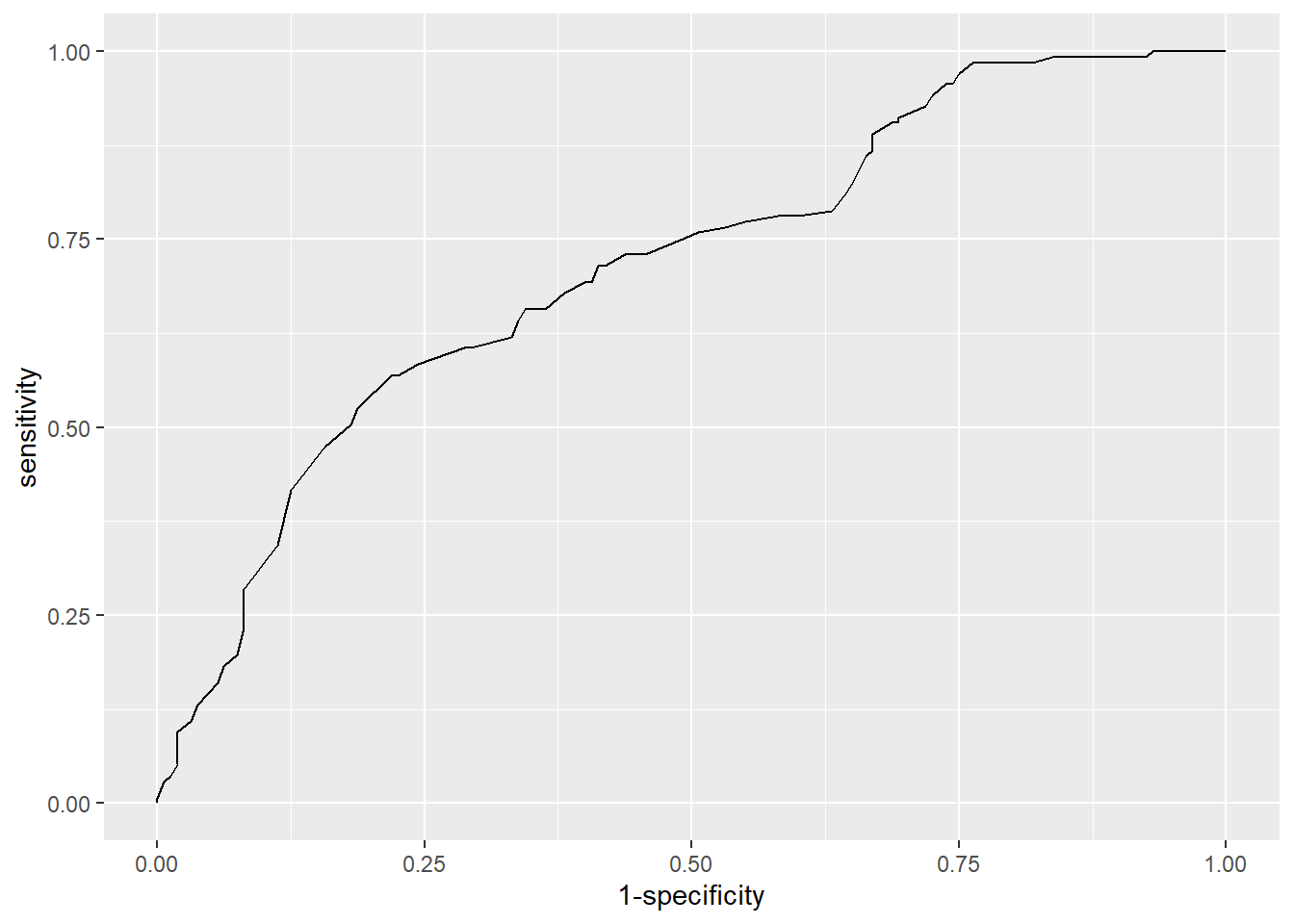

res$auc

Area under the curve: 0.713

# plot ROC curve with AUC in title
ggroc(res, legacy.axes = TRUE) +
  labs(title = paste0("AUC = ", round(res$auc, 2)))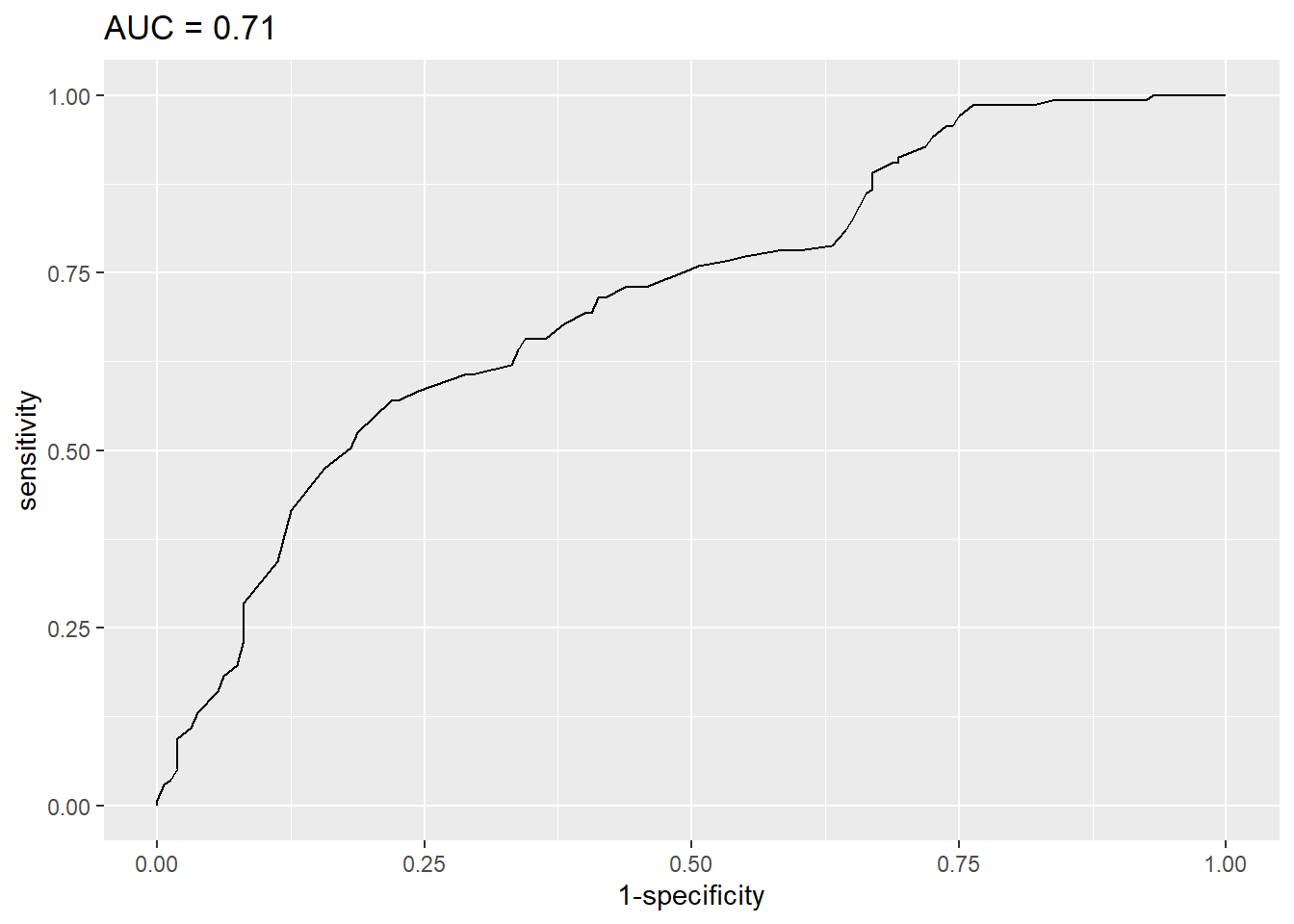

library(gtsummary)

# print table of results
tbl_regression(m3, exponentiate = TRUE)

Characteristic	OR¹	95% CI¹	p-value
sex
female	—	—
male	4.47	2.57, 8.05	<0.001
age	1.07	1.04, 1.10	<0.001
¹ OR = Odds Ratio, CI = Confidence Interval

library(finalfit)
# set variables
dependent <- "heart_disease"
independent <- c("age", "sex")
independent_final <- c("age", "sex", "chest_pain")

dat %>% or_plot(dependent, independent,
  table_text_size = 3.5 # reduce text size
)